Studies Showing That Longevity Tends to Run in Families Validate:

• Research article
• Open Access
• Published: 06 January 2021

Improved selection of participants in genetic longevity studies: family scores revisited

• Niels van den Berg²,
• Michel H. Hof³,
• Marian Beekman² &
• Eline Slagboomⁱⁱ

BMC Medical Research Methodology volume 21, Article number:7 (2021) Cite this article

• 753 Accesses

• 1 Citations

• Metrics details

Abstract

Background

Although human longevity tends to cluster within families, genetic studies on longevity take had express success in identifying longevity loci. One of the main causes of this express success is the pick of participants. Studies generally include sporadically long-lived individuals, i.e. individuals with the longevity phenotype but without a genetic predisposition for longevity. The inclusion of these individuals causes phenotype heterogeneity which results in power reduction and bias. A way to avert sporadically long-lived individuals and reduce sample heterogeneity is to include family history of longevity as pick criterion using a longevity family unit score. A chief challenge when developing family scores are the large differences in family unit size, because of existent differences in sibship sizes or because of missing data.

Methods

Nosotros discussed the statistical properties of two existing longevity family scores: the Family Longevity Selection Score (FLoSS) and the Longevity Relatives Count (LRC) score and we evaluated their performance dealing with differential family size. We proposed a new longevity family unit score, the mLRC score, an extension of the LRC based on random furnishings modeling, which is robust for family size and missing values. The performance of the new mLRC as selection tool was evaluated in an intensive simulation study and illustrated in a big existent dataset, the Historical Sample of the Netherlands (HSN).

Results

Empirical scores such as the FLOSS and LRC cannot properly deal with differential family unit size and missing information. Our simulation study showed that mLRC is not affected by family size and provides more accurate selections of long-lived families. The analysis of 1105 sibships of the Historical Sample of the Netherlands showed that the choice of long-lived individuals based on the mLRC score predicts excess survival in the validation set ameliorate than the selection based on the LRC score .

Conclusions

Model-based score systems such equally the mLRC score help to reduce heterogeneity in the selection of long-lived families. The power of future studies into the genetics of longevity tin probable be improved and their bias reduced, by selecting long-lived cases using the mLRC.

Peer Review reports

Background

At that place is strong evidence that longevity, defined equally survival to extreme ages, clusters within families and is transmitted across generations [1,2,iii,4,5,vi,7]. Recent research [5] on two large population-based multi-generational family studies indicates that longevity is transmitted as a quantitative genetic trait. Moreover, associations betwixt environmental factors and familial clustering have been rarely found using historical pedigree information [five, viii,ix,10]. Although these findings suggest that human longevity has a genetic component, genetic studies on longevity accept had limited success in identifying longevity loci [11,12,13,xiv,15,16,17]. One of the principal causes for this limited success could be the large heterogeneity in criteria for participant selection in longevity studies [5, xviii, 19]. Since the study participants must be live to extract blood or other biomaterials their longevity phenotype is, by definition, unknown. An additional complication of longevity studies is the ongoing increment in life expectancy due to non-genetic factors [twenty], such equally improvements in nutrition, life style and wellness intendance. If but individual age is considered as choice benchmark, these non-genetic factors increase the risk of including sporadically long-lived individuals i.e. individuals with the longevity phenotype but who do not have an underlying genetic predisposition for longevity.

To obtain a sample with less phenotype heterogeneity, the family history of longevity can be used as a participant selection criterion [five, xviii]. Although this arroyo does not avert that sample option is influenced by family-shared non-genetic factors potentially involved in longevity, it is probable that information technology increases the power in instance-command studies to detect novel genetic loci [21, 22]. A natural style to incorporate family unit history in the study design is to develop a longevity family score to identify families with the heritable longevity trait and to subsequently select live members of these families for (genetic) longevity studies. A number of longevity family scores have been previously proposed [iv, 18, 23,24,25], using different definitions of individual longevity and different means of summarizing longevity within families. The implications of these choices are not well understood, namely how the coaction amidst private longevity definition, family-specific summary measures and family size affects the sample selection procedure based on longevity family scores. The first claiming when developing longevity family scores is defining individual longevity. It is unclear how extreme the age at death must be to label an private as long-lived and which calibration is nearly beneficial and then that scores reflect differences in extreme survival and non just in overall lifespan. The second challenge when developing longevity family unit scores are the large differences in family size. These differences imply that the available information per family differs. For a family unit with 12 members, for example, more information is available than for a family with ii members simply. Chiefly, we typically do not know whether these differences are real differences in sibship sizes or the result of missing information caused by limitations of the data collection. If not properly addressed, differences in family size can lead to biased rankings of long-lived families. This can lead to an increased heterogeneity among selected participants in longevity studies and hence reduce power of analyses. Instead of studying the genetics of longevity, biased selections tin can potentially lead to the combined analysis of the genetics of longevity, fertility and other factors affecting family size, such equally, for example, socio economic status. Upwards till now, this important challenge has not received plenty attention and how to address this problem even so remains open.

In this newspaper, we investigate to what extent existing longevity family scores such as the Family Longevity Selection Score (FLoSS) [23] and the Longevity Relatives Count (LRC) score [18], are afflicted past differential family size. After, we propose an alternative method based on mixed effects regression modelling to deal with differences in family unit size when building a longevity family score.

The primary novelty of our new approach is to consider the family size as a source of doubtfulness when estimating the level of longevity of a family unit. Hence, we propose to select families accounting for such estimated uncertainty. This new approach volition contribute to more robust scores and pick rules in longevity studies.

Methods

Existing longevity family unit scores and family size

Several longevity or excess survival family scores take been previously proposed [4, 18, 23,24,25]. Frequently, to measure private survival exceptionality, age at death is transformed to the respective survival percentile [18] or related measure out such as the cumulative hazard [4, 23, 25] using life table data of a reference population, typically matching for sex and nascence accomplice. An alternative approach based on defining private survival exceptionality equally the difference between individual's age at death and the sample-based expected historic period at death correcting for a number of confounders has been too proposed [24].

Nosotros focus on two of the previous proposals, representative of two dissimilar means of summarizing individual survival exceptionality within families: the Family Longevity Selection Score (FLoSS) [23] and the Longevity Relatives Count (LRC) score [18]. The FLoSS relies on a sum to summarize survival exceptional within families, while the LRC score is representative of the residuum of previously proposed longevity scores which all rely on an empirical expectation every bit summary, i.east., the mean [4, 24, 25] or a proportion [18] depending on the nature of the individual measure of survival exceptionality. These ii type of summary measures (sum versus empirical expectation) have different implications with regard to the influence of family size in the resulting scoring system.

The FLoSS favors large families

The Family unit Longevity Selection Score (FLoSS) [23] was synthetic using siblings included in the Long Life Family unit Report. The FLoSS is a modification of the SE _f score which adds a bonus for the presence of living family unit members. Since the main backdrop of SE _f transfer to FLoSS, for the sake of simplicity nosotros focus on the properties of the SE _f , divers, for each family unit i, every bit follows:

$$ {SE}_{fi}=\sum \limits_{j=1}^{N_i}{SE}_{ij}=\sum \limits_{j=i}^{N_i}\left(-\mathit{\log}\left(S\left({t}_{ij}|{bc}_{ij},{sex}_{ij}\right)\correct)-1\correct)=\sum \limits_{j=i}^{N_i}\left(\varLambda \left({t}_{ij}|{bc}_{ij},{sex}_{ij}\correct)-1\right), $$

where t _ij is the age at death of family member j of family i, with j = ane,…,N _i members, S(t _ij |bc _ij , sexual practice _ij ) is the survival probability at age t _ij given sex and birth cohort in the reference population and Λ(t _ij |bc _ij , sex _ij ) is the respective cumulative run a risk. SE _ij varies between − 1 (if South(t _ij |bc _ij , sexual practice _ij ) = 1) and ∞ (if S(t _ij |bc _ij , sex _ij ) = 0). The maximum value of SE _ij is determined by the maximum age recorded in the used life table. If for instance, this maximum age at expiry is 99, like in the Dutch life tables [26], and the minimum survival in the population is South(99|bc _ij , sexual practice _ij ) = 0.01, this provides a maximum SE _ij  = 4.half-dozen. The reference value, corresponding to a value SE _ij  = 0 corresponds to South(t _ij |bc _ij , sexual activity _ij ) = 0.37. This means that family unit members with age at expiry beyond the top 37% survivors count positively in the score and those with younger ages at death count negatively. For example, using the Dutch life tables, this cutting-off would correspond, for those born around 1900 with an historic period of death of around 73 years for men and of around 80 for women. This thresholds are not in line with contempo evidence indicating that college ages at death need to be considered to capture the heritable longevity trait [5, 18]. This problem tin can exist solved by workout survival to beingness live at sure age. For instance, a conditioning age of 40 years has previously been proposed [23], which increases the age cut-off associated to SE _ij  = 0. For example, using Dutch lifetables this would stand for to a cut-off of around 84 years for women and 78 year for men for individuals born effectually 1900. These ages represent with percentiles survivals at birth of around 0.28 (oldest 28% survivors of their nascency cohort) which are likely not extreme enough to capture the heritable longevity trait. This drawback is somehow compensated past the strongly skewed distribution of SE _ij , meaning that the touch on of increasing, for example, from 95 to 96 years is greater than the increment from seventy to 71.

An additional problem of the SE _f score is that information technology uses the sum over the available family members to summarize the level of survival exceptionality within the family. This implies that big families are systematically overweighted when using SE _f . This phenomenon is illustrated in Fig. one. Three example populations with twenty sibships each and unlike level of enrichment for longevity are considered. In the 3 examples, we consider sibships of increasing size, N _i = i + 1, i = one,2,...,twenty. In the first case population, all sibships take ii siblings belonging to the summit 5% survivors of their sex-specific nascency accomplice and the balance of siblings belonging to the top 30% survivors, and so these family members are conspicuously non long-lived. In the second, all sibships accept two siblings belonging to the top 10% survivors of their sex activity-specific birth accomplice and the residue of siblings belonging to the top xxx% survivors. In the third example population all siblings belong to the height 30% survivors, representing a population with no long-lived individuals. The left panel of Fig. i illustrates the functioning of the score SE _f in these three examples. Overall, increasing the sibship size leads to larger values of SE _f . Moreover, larger families with lower proportions of long-lived members tin can nowadays a larger value of SE _f than modest families with a larger proportion of long-lived members. For case, a family with 2 members belonging to the acme x survivors and 8 extra not long-lived siblings has a larger SE _f than a family with ii members in the top 10 survivors and five extra not long-lived siblings (black line). Information technology can also happen that a large family where two siblings are top ten% survivors and the rest non long-lived present a larger SE _f than a smaller family where ii siblings are acme v% and the rest are not long-lived. The increasing pinkish line corresponding to the third scenario illustrates that large families with no long-lived family members can nowadays large values of SE _f , with SE _f arbitrarily increasing in parallel to family size.

Fig. i

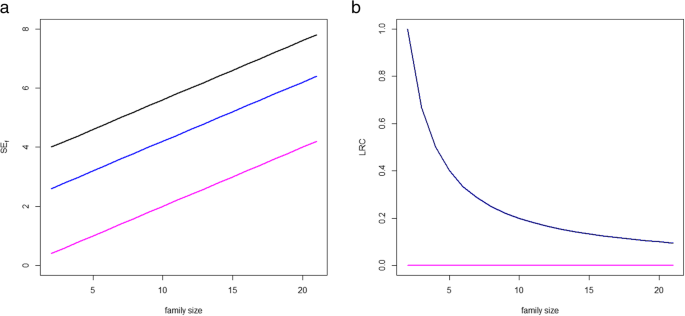
Instance of iii hypothetical populations with twenty sibships with sizes Due north_i = ii,iii,...,21. In each population families are ranked according to Due south E _f (left panel) and LRC (correct panel). The black lines represents a population in which all families have two siblings belonging to the superlative five% survivors (long-lived) of their sex-specific nascency cohort and the rest of siblings belonging to the pinnacle 30% survivors (not long-lived). The blue lines represent a population in which all families have 2 siblings belonging to the tiptop 10% survivors (long-lived) of their sex-specific birth cohort and the remainder of siblings belonging to the top xxx% survivors. The pinkish lines represent a population equanimous of families with all family members not log-lived, belonging to the pinnacle 30% survivors. The left panel shows the value of S E _f with increasing number of non-lived family members. The correct panel shows the value of LRC with increasing number of non-lived family members. Because of the definition of LRC, black and blueish lines coincide in the correct panel

Full size image

In summary, using SE _f and FLoSS in the option of long-lived families may atomic number 82 to an overrepresentation of large families and hence undesirable heterogeneity in the selected sample of families. Importantly, the size of the families governs the range of variation of the family unit score implying that SE _f and FLoSS are not comparable when calculated in populations with different underlying family unit size patterns. Since this is an highly undesired feature, nosotros will not farther focus on the SE _f score (and FLoSS) in the rest of the newspaper.

The LRC score favors small families

To mitigate the previously explained bias towards large families, a solution is to utilize a different summary measure out at the family unit level, like the average [4, 25].

In this line, and based on the results of a recent study which shows that longevity is heritable beyond the x% survivors of their nascency cohort [5], the Longevity Relatives Count (LRC) score has been proposed [xviii]. The original definition of the LRC score allows for the inclusion of family members with different caste of relatedness. Here, nosotros focus on its simplest form considering but siblings in its construction:

$$ {LRC}_i=\frac{\sum \limits_{j=one}^{N_i}I\left({P}_{ij}\ge 0.9\right)}{N_i} $$

(1)

where P _ij is the sex and birth cohort specific percentile survival of individual j of family i, i.e., P _ij  = ane −S(t _ij |bc _ij ,sex _ij ). I(P _ij  ≥ 0.nine) is a variable indicator taking value 1 if individual j belongs to the top 10 survivor of his/her sex-specific birth cohort and 0 otherwise. Every bit a result, LRC _i is the proportion of members of family i belonging to the group of pinnacle 10 survivors, defined every bit long-lived. The LRC is bounded between 0 and i, providing a clear interpretation and comparability beyond populations. A drawback is that it is based on a binary definition of longevity, ignoring differences in longevity beyond the superlative 10% of survivors.

The LRC score is based on calculating a proportion, and as a effect, the resulting ranking based on this score indirectly favors small families. For small families, it is more easy to accept 100% of its family members in the acme x% survivors for than big families. Hence, in small families information technology can be questioned whether a large LRC truly captures the heritable longevity trait.

The problem of this approach is of different nature than the instance of the SE _f score. While adding non long-lived family unit members implies an increase in SE _f , this is not the case for LRC (Fig. 1, right console). Instead of a systematic bias, we at present face a trouble of different uncertainty levels depending of the size of the family which cannot be properly captured by an empirical proportion. Consider the following instance for illustration. Two families, both with half of the siblings long-lived, only in the starting time case the sibship size was 2 and on the second case the sibship size was 10. It is articulate that there is more data in the second case and hence the ranking should besides have this into account. However, using empirical proportions small families are benefitted.

Accounting for uncertainty in longevity family scores

To deal with the heterogeneity in information between families caused by their size, we propose to use mixed effects regression modelling in the interpretation of family scores. In particular, we focus on the LRC, and extend its concept by introducing family specific random effects.

Let Y _ij  =I(P _ij ≥ c) be a binary random variable that indicates if P _ij is equal of larger than c, where P _ij is the percentile survival of individual j of family i, and c is a pre-specified threshold of longevity. For case, c = 0.90. Let u _i be a random consequence shared by the members of the same family that reflects the unobserved factors contributing to longevity.

Bold that Y _ij follows a Bernoulli distribution, the family specific probability to reach c is given past the post-obit logistic regression model with random intercept:

$$ {p}_i=P\left({Y}_{ij}=one|{u}_i\right)=\frac{e^{\beta_0+{u}_i}}{ane+{e}^{\beta_0+{u}_i}} $$

(2)

We presume that u _i follows a normal distribution with mean zero and variance σ ². And so, the parameters β ₀ and σ ² can exist estimated maximizing the resulting likelihood role \( \prod \limits_{i=1}^N{L}_i\left({\beta}_0,\sigma \right)=\int \prod \limits_{j=one}^{N_i}P{\left({Y}_{ij}=1|{u}_i\right)}^{y_{ij}}{\left(one-P\left({Y}_{ij}=i|{u}_i\right)\right)}^{\left(1-{y}_{ij}\right)}f\left({u}_i;{\sigma}^2\right)d{u}_i \), where North is the total number of families, N _i is the number of family members of family i and f is the density function of u _i . Maximization of the likelihood cannot be analytically solved and requires numerical approximation techniques (e.1000. quadrature methods).

Finally, we tin obtain \( {\hat{p}}_i \), the expected value of p _i given the observed data of family i and the estimated β ₀ and σ, denoted by \( {\chapeau{\beta}}_o \) and \( \chapeau{\sigma} \), as

$$ {\hat{p}}_i={\int}_{-\infty}^{\infty}\frac{east^{{\lid{\beta}}_0+u}}{ane+{e}^{{\chapeau{\beta}}_0+u}}\ f\left(u|{y}_{i1},\dots, {y}_{i{N}_i},{\hat{\beta}}_0,\chapeau{\sigma}\right) du $$

(three)

where \( f\left(u|{y}_{i1},\dots, {y}_{i{N}_i},{\hat{\beta}}_0,\hat{\sigma}\right) \) is the density of the posterior distribution of the family unit specific random consequence. Using Bayes' rule, this density tin can be obtained every bit

$$ f\left(u|{y}_{i1},\dots, {y}_{i{N}_i},{\hat{\beta}}_0,\hat{\sigma}\right)=\frac{f\left({y}_{i1},\dots, {y}_{i{North}_i}|{\lid{\beta}}_0,u\right)f\left(u|\lid{\sigma}\correct)}{\int_{-\infty}^{\infty }f\left({y}_{i1},\dots, {y}_{i{N}_i}|{\lid{\beta}}_0,u\right)f\left(u|\lid{\sigma}\right) du} $$

where \( f\left({y}_{i1},\dots, {y}_{i{N}_i}|{\hat{\beta}}_0,u\right)=\prod \limits_{j=i}^{N_i}P{\left({Y}_{ij}=1|{u}_i\correct)}^{y_{ij}}{\left(1-P\left({Y}_{ij}=1|{u}_i\correct)\correct)}^{\left(1-{y}_{ij}\correct)} \).

We propose to consider \( {\hat{p}}_i \) as a new longevity family score of family unit i, and nosotros announce information technology by mLRC _i . In this way, mLRC can be regarded as a model-based version of LRC which includes shrinkage based on N _i . mLRC _i tin can however exist interpreted as the proportion of long-lived members of family i but it captures the doubtfulness due to family size by the different 'weight' each family unit receives through its estimated random event \( {\hat{u}}_i \).

Software implementation

The new mLRC family score, together with the LRC and FLoSS take been implemented in R. The code is provided as supplementary material.

Results

Simulation study

Faux data is generated under the assumption that a latent factor, shared by the members of the same family, controls the degree of longevity of the family. Based on the false information, we tin mensurate the level of agreement betwixt the underlying longevity gene and different longevity family scores.

Characteristics of the simulated datasets such as the number and size of the families are chosen to mimic our existent information set. In each run of the simulation, we false Due north = g families of different sizes, namely 200 families with respectively size 2,3,eight,10, and 14 individuals. For each private j of family i, where i = 1,...,Due north, we sampled survival percentiles p _ij from a beta distribution with parameters a = exp.(0.1) and b =a × exp.(−(1 +u _i )), where u _i was a random effect common to the N _i members of family i. The random effect was sampled from a normal distribution with mean 0 and standard deviation ii. Big values of u _i decreased the survival percentile p _ij , which meant that the families with the lowest values of the random effect were the most enriched for longevity.

For each family, we computed the LRC score and the new model-based LRC (mLRC). Both scores were compared in terms of their relation with family size and operation equally pick tools. The simulation was repeated 1000 times.

Table 1 shows the distribution of family size according to the values of LRC and mLRC. The LRC score is strongly affected by family unit size; families with low sibship sizes tend to have large values of LRC (left column of Table i). No clear relation betwixt family size and mLRC is observed (right column of Tabular array 1), which is in agreement with the data generation mechanism. Figure 2 shows the comparison between the LRC and mLRC for all the families in one simulation run. For small families, the mLRC score is typically lower than the LRC score when the LRC score is large. This is caused by the penalisation of our new method due to lack of information in small families. Analogously, small families are weighted upwards when the LRC score is low post-obit the aforementioned principle of major uncertainty when the family size is small-scale. Still, if the level of exceptionality of the observed family members is big, small families tin can all the same outperform large families. This is illustrated by small families (for example, with N _i  = ii, red dots) appearing at the correct role of the graphic in Fig. two. The power of mLRC to correctly bargain with differences in family size, explains that the clan between family unit size and the mLRC score is very low (correct column Table 1).

Table 1 Family size and family scores in false information

Full size table

Fig. ii

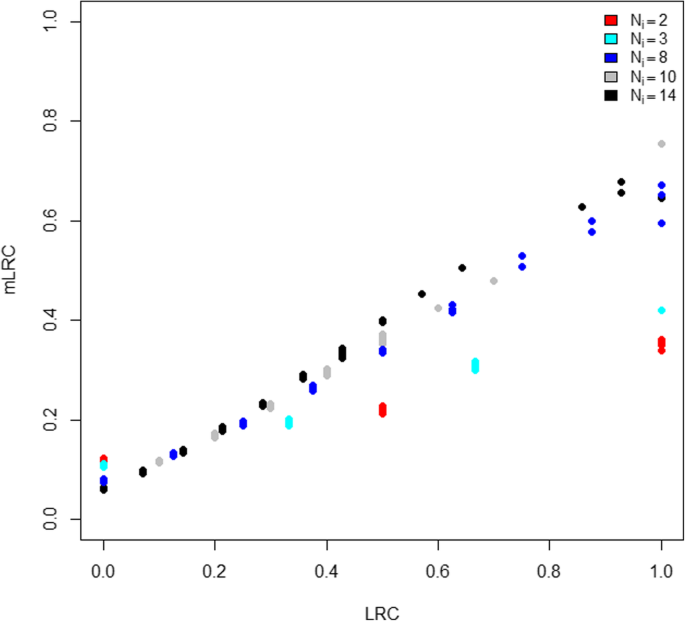
Comparing of LRC and mLRC with false data. For each of the N = m families in 1 simulation run, we display the LRC score (x-axis) against the mLRC score (y-axis). Every signal in the graphic represents a family unit, colored according to its size. Red dots represent families of size N_i = 2, calorie-free blue dots stand for families of size North_i = iii, dark bluish dots represent families of size N_i = viii, grey dots represent families of size North_i = 10 and black dots represent families of size Due north_i = 14

Total size image

To evaluate the functioning of selection rules based on the LRC and mLRC scores, we considered two definitions of longevity. First, the 10% of families with the lowest value of the random effect u were divers equally truly long-lived. Second, we considered the 5% of families with the lowest value of the random outcome u equally truly long-lived. For both definitions, we checked the agreement between the truly long-lived families and the selected families based on the LRC and mLRC scores. To perform this selection, the families with the ten% (respectively 5%) largest LRC or mLRC score were labeled equally long-lived. Since our main interest was to avoid families not enriched for longevity in our option, we used the positive predictive value (PPV) as summary measure of our simulations. The PPV is defined as the proportion of truly long-lived families among those classified as long-lived using the score-based choice rule under investigation.

Figure 3 shows the distribution of the positive predictive values from the thousand simulation runs. When defining the x% of families with the lowest value of the random effect u as truly long-lived (left panel of Fig. three), the mean PPV for the selection based on LRC was 54% (sd = 4%), meaning that on average, among the thou meridian 10% families classified as long-lived according to LRC, 54% were truly long-lived. The mean PPV increased to 62% (sd = 4%) when using mLRC for option of the tiptop x% families. If we focus on the top 5% families (right panel of Fig. three), the average accuracy of the selection based on LRC decreased (mean PPV = 0.52,sd = 0.xiii). In addition, we establish large variability of the PPV among simulation runs, which indicates instable performance of the LRC score. On the opposite, the accuracy based on mLRC increased in this instance (mean PPV = 0.67, sd = 0.06). These results show that selection of families based on mLRC clearly outperforms selection based on LRC.

Fig. iii

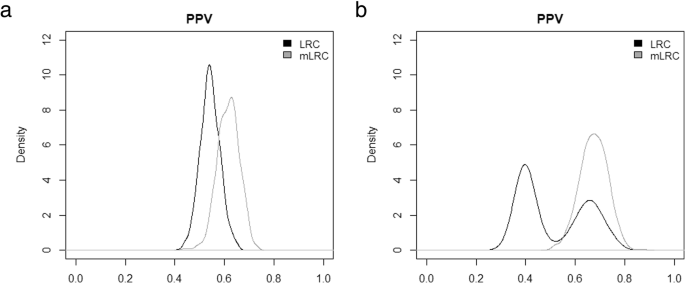
Evaluation of LRC and mLRC equally selection tools with fake data. Distribution of positive predictive (PPV) values across 1000 simulation runs. For each simulation run, the PPV associated to the selection rule under investigation was computed. Black lines represent the results based on LRC and grey lines represent the results based on mLRC. The left panel shows the results when defining the ten% of families with the lowest value of the random effect u as truly long-lived and the pick criterion is declaring families with the 10% largest values of the score as long-lived. The right panel shows the results for the more strict definition of longevity, based on the 5% lowest values of the random event u and the selection criterion is declaring families with the 5% largest values of the score as long-lived

Total size image

Real data: the historical sample of kingdom of the netherlands

The Historical Sample of holland (HSN) Long Lives report [27, 28] is an all-encompassing database which contains lifetime data for the members of 1326 5-generational families, evolving around a unmarried proband (Index Person, IP) per family unit [29]. Nosotros focus on the siblings present in the second (F2) generation which are the children of the IPs. The choice for a part of these IPs was enriched for longevity. Specifically, the selected IPs were part of a case-control report to compare differences in longevity amid descendants of 884 IPs who died at 80 years or beyond (case group) and 442 IPs who died between 40 and 59 years (control group) [18, thirty]. After removing individuals with missing age at decease, unmarried child sibships, and individuals belonging to non-extinct birth cohorts past the date of data collection (death dates were updated at 2017 and 110 years was gear up equally maximum age); the last sample of our analysis consisted of 1105 sibships, children of the same HSN IPs, which corresponded to 5361 individuals.

To evaluate the functioning of the new longevity family score mLRC and compare it to the original LRC, we first randomly selected a sample of contained individuals by choosing 1 private at random from each of the 1105 bachelor sibships. This set of independent individuals was set up bated from the score calculations and subsequently used every bit a validation set up to evaluate score performance. This validation set resembles the potential candidates to exist included in, for case, a GWA study of longevity. Then, LRC and mLRC were calculated based on a sample of 4256 individuals. Afterwards, based on both scores nosotros conducted a selection of long-lived families and nosotros checked if those corresponded with a survival benefit in the validation gear up using Cox proportional hazard regression.

The sibship size was highly varying in the sample (Fig. 4). As expected, LRC is largely afflicted by family size, and families with large values of LRC nowadays lower sibship sizes (Tabular array 2). Nosotros do not observe a blueprint in family size co-ordinate to the estimated level of familiar longevity using mLRC. Figure 5 shows the distribution of the LRC and mLRC scores in the analyzed sibships of the HSN dataset.

Fig. 4

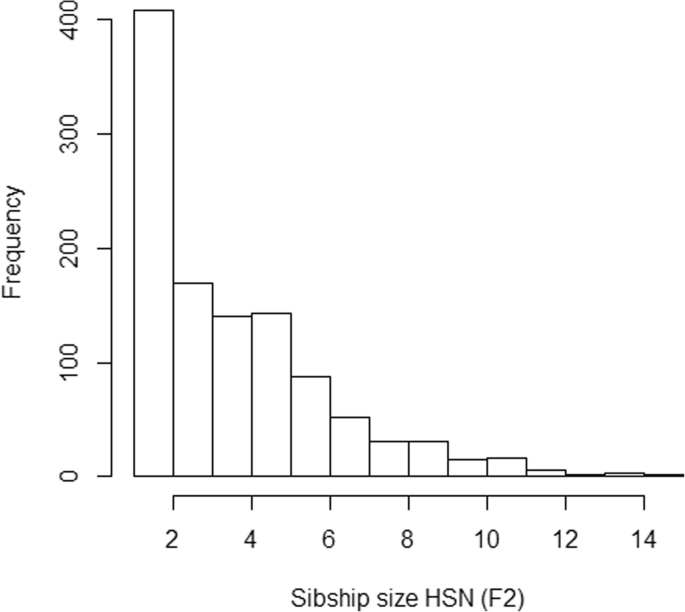
Sibship size in the HSN data

Full size image

Table 2 Family unit size and family unit scores in the HSN data

Full size tabular array

Fig. 5

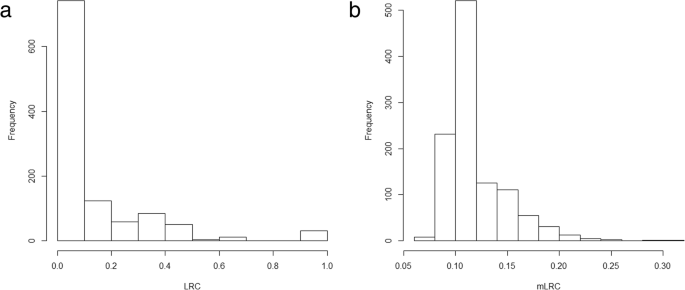
Distribution of the LRC (left panel) and mLRC (right panel) scores in the analyzed sibships of the HSN dataset

Full size image

Previous literature [18], has suggested LRC ≥ 0.three every bit a selection criterion to capture the heritable longevity trait. In our sample, LRC ≥ 0.3 corresponds to the selection of the 15% families with the largest values of the LRC score. We evaluated the performance of this choice criterion by comparison the survival of the individuals of the validation set belonging the selected families to the rest of individuals in the validation set. Analogously, we selected the meridian 15% families according to ranking resulting from using the mLRC equally longevity score which corresponds to ascertain families with mLRC ≥ 0.fifteen every bit long-lived and evaluated this selection strategy using the validation set up. For each of the proposed selections, we fitted a Cox regression model with the each of the pick indicators equally explanatory variables. Both models were adjusted past gender and nascence cohort. Tabular array 3 shows that the choice of long-lived individuals based on the mLRC score predicts excess survival in the validation ready improve than the selection based on the LRC score (β _{LRC ≥ 0.3}  = − 0.287, β _{mLRC ≥ 0.xv}  = − 0.321).

Tabular array 3 Evaluation of selection strategies of long-lived families based on LRC and mLRC scores in the HSN

Full size table

Discussion

Nosotros proposed a method based on mixed effects regression modelling to estimate longevity family scores and properly account for differences in family size when ranking families according to their longevity and apply this ranking for the selection of participants in longevity studies. Our simulation written report and real data analysis show that the new proposed approach (mLRC) yields improve results than its empirical counterpart (LRC) in terms of selection of long-lived individuals. Nosotros showed that the SE _f score and FLoSS increase with the add-on of non-long-lived family members and their interpretation is ruled by the underlying family size distribution. We also showed that the LRC score puts too much weight on pocket-sized, less-informative families. The mLRC score was non afflicted by sibship size and therefore its resulting ranking better predicted the survival of 1105 independent study participants. The new mLRC score seems to reduce heterogeneity in the pick of families and its awarding could potentially help to improve power and bias reduction in longevity studies.

Our current arroyo has some limitations. First, the binary nature of the current mLRC discards important information which could contribute to improve its performance. An interesting property of the SE _f score and the FLoSS is their continuous nature. Other continuous longevity family unit scores have been previously proposed [4, 24, 25]. The Longevity Family Score (LFS) [iv] and the Family Mortality History Score (FMHS) [25] are closely related to the SE _f and FLoSS since all use the aforementioned measure of private survival exceptionality based on transforming the observed ages at death to survival percentiles in a reference population using life tables. The FMHS is restricted to parental data and hence non bailiwick to differential family size. The LFS, the SE _f and the FLoSS are extensions of the FMHS which can deal with sibships of arbitrary size. The Familial Excess Longevity (FEL) score [24] is also continuous but it does rely on population life tables. Instead, individual survival exceptionality is divers as the difference between observed and expected age, derived from an accelerated failure time regression model. Both the LFS and the FEL scores are based on the mean every bit family-specific summary measure out and hence share with the LRC score the discussed limitations of empirical expectations.

A potential drawback of all these continuous longevity scores is that relatively young family unit members can contribute positively to these scores. Even subsequently workout on being older than 40 as proposed for the FLoSS, the resulting score is probably influenced by ages at death which are not extreme plenty to capture the heritable longevity trait. Evidence of this is supported by studies that take pointed towards increasing family aggregation of survival when focusing on more extreme ages at death for longevity definition [thirteen, 31] and contempo publications indicating that the longevity trait seems to be heritable considering lifespan thresholds across the peak 10% survivors of a given birth accomplice [5]. A model-based modified version of SE _f or the LFS which minimizes the contribution of young family unit members seems a promising line of future inquiry. Still, the extremely skewed distribution of the private measure of longevity of these scores makes the extension of our method not straightforward.

Another important topic is dealing with alive or lost on follow-up (right censored) individuals when amalgam longevity family scores. We have assumed total observation of lifespan of siblings included in the calculation of the score, and then scores can be regarded as family history scores of alive relatives who could potentially be selected to participate in a (genetic) longevity study.

The FLoSS score is the extension of the discussed score SE _f to permit for the inclusion of correct censored observations. The FLoSS follows a single imputation approach based on imputing live individuals with the sex and nascence cohort specific conditional expected age at decease. This is an example of unmarried imputation which underestimates the uncertainty of estimates and can potentially lead to bias. More than avant-garde methods are possible in the mixed effect setting and its inclusion is left every bit subject of future research. Finally, contempo evidence [9] indicates that the inclusion of family members of different degree of relatedness is of not bad importance to capture the heritable longevity phenotype and hence the proposed method should likewise exist extended to this more circuitous setting.

Finally, it is important to mention that our approach may result in selections that are influenced past family-shared non-genetic factors. Despite previous research based on historical pedigree data take led to picayune show for associations between non-genetic factors such equally socio-economic status, fertility factors or religious denomination and familial longevity [5, 8,9,10], other socio-behavioral and environmental factors such as personality and lifestyle may influence familial clustering of longevity. Since many of these likewise have a strong genetic component itself it is near likely that gene ecology interactions tin can explain a part of the familial clustering of longevity. Still in this complex setting, the employ of well-designed family scores is expected to reduce genetic heterogeneity and contribute to a power increase in case-control longevity studies to detect novel genetic loci. Moreover, our mLRC score can exist applied in more than general longevity studies devoted to investigate the interplay among genetic and not-genetic factors involved in longevity.

Conclusions

To properly account for differences in family size is of paramount importance when deriving family scores of longevity and using them for ranking families and selecting participants in longevity studies. The methodology described in this paper is therefore of cracking relevance and can help to better selection of participants in future longevity studies.

Availability of data and materials

The data used for this written report will be made freely available at the Data Archiving and Networked Services (DANS) repository but are currently not even so publicly available due to ongoing checks to guarantee that the information sharing process is in accord with Dutch and international privacy legislation. Data are withal available from the authors upon reasonable request.

Abbreviations

FLoSS:

Family Longevity Selection Score

FMHS:

Family unit Mortality History Score

HSN:

Historical Sample of kingdom of the netherlands

IP:

Index person

LFS:

Longevity Family Score

LRC:

Longevity Relatives Count

mLRC:

model-based Longevity Relatives Count

PPV:

Positive predictive value

SE_f :

Survival Exceptionality

Sd:

Standard deviation

References

1. van den Berg N, Beekman G, Smith KR, Janssens A, Slagboom PE. Historical demography and longevity genetics: Dorsum to the futurity. Ageing Res Rev. 2017;38:28–39.

   Commodity  Google Scholar

2. Herskind AM, et al. The heritability of human longevity: a population-based report of 2872 Danish twin pairs born 1870–1900. Hum Genet. 1996;97:319–23.

   CAS  Article  Google Scholar

3. Perls TT, et al. Life-long sustained mortality advantage of siblings of centenarians. Proc Natl Acad Sci. 2002;99:8442–seven.

   CAS  Article  Google Scholar

4. van den Berg N, et al. Longevity around the plough of the 20th century: life-long sustained survival advantage for parents of Today's nonagenarians. J Gerontol Ser A. 2018;73:1295–302.

   Article  Google Scholar

5. van den Berg N, et al. Longevity divers as top 10% survivors and beyond is transmitted as a quantitative genetic trait. Nat Commun. 2019;x:35.

   Article  Google Scholar

6. Schoenmaker Chiliad, et al. Prove of genetic enrichment for infrequent survival 595 using a family approach: the Leiden longevity study. Eur J Hum Genet. 2006;14:79–84.

   Article  Google Scholar

7. Ljungquist B, Berg Southward, Lanke J, McClearn GE, Pedersen NL. The consequence of genetic 597 factors for longevity: a comparison of identical and fraternal twins in the Swedish 598 twin registry. J Gerontol Ser A Biol Sci Med Sci. 1998;53:441–6.

   Commodity  Google Scholar

8. Yous D, Danan G, Yi Z. Familial transmission of human longevity among the oldest-old in Communist china. J Appl Gerontol. 2010;29:308–32.

   Article  Google Scholar

9. Gavrilov LA, Gavrilova NS. Predictors of exceptional longevity: effects of early-life and midlife weather, and familial longevity. Due north Am Actuar J. 2015;19:174–86.

   Article  Google Scholar

10. Mourits RJ, et al. Intergenerational transmission of longevity is not affected past other familial factors: prove from 16,905 Dutch families from Zeeland, 1812-1962. Hist Fam. 2020;25:484–526.

    Article  Google Scholar

11. Deelen J, et al. A meta-analysis of genome-broad association studies identifies multiple longevity genes. Nat Commun. 2019;10:3669.

    Article  Google Scholar

12. Shadyab AH, LaCroix AZ. Genetic factors associated with longevity: a review of 615 contempo findings. Ageing Res Rev. 2015;19:ane–vii.

    CAS  Article  Google Scholar

13. Slagboom EP, van den Berg North, Deelen J. Phenome and genome based 617 studies into human ageing and longevity: an overview. Biochim Biophys Acta Mol Basis Dis. 1864;2018:2742–51.

    Google Scholar

14. Deelen J, et al. Genome-wide association meta-analysis of homo longevity 620 identifies a novel locus conferring survival beyond 90 years of age. Hum Mol Genet. 2014;23:4420–32.

    CAS  Article  Google Scholar

15. Sebastiani P, et al. Four genome-broad association studies identify new 635 farthermost longevity variants. J Gerontol A Biol Sci Med Sci. 2017;72:1453–64.

    CAS  Article  Google Scholar

16. Flachsbart F, et al. Immunochip analysis identifies association of the 637 RAD50/IL13 region with man longevity. Crumbling Jail cell. 2016;15:585–8.

    CAS  Article  Google Scholar

17. Zeng Y, et al. Novel loci and pathways significantly associated with longevity. Sci Rep. 2016;6:21243.

    CAS  Article  Google Scholar

18. van den Berg N, et al. Longevity Relatives Count score defines heritable longevity carriers and propose example improvement in genetic studies. Crumbling Cell. 2020;xix:e13139.

19. Sebastiani P, Nussbaum L, Andersen SL, Black MJ, Perls TT. Increasing Sibling Relative Risk of Survival to Older and Older Ages and the Importance of Precise Definitions of "Crumbling," "Life Span," and "Longevity". J Gerontol Ser A Biol Sci Med Sci. 2016;71:340–six.

    Article  Google Scholar

20. Oeppen J, Vaupel J. W. Demography. Broken limits to life expectancy. Science. 2002;296:1029–31.

    CAS  Article  Google Scholar

21. Liu JZ, Erlich Y, Pickrell JK. Case–command association mapping by proxy using family history of affliction. Nat Genet. 2017;49:325–31 https://doi.org/10.1038/ng.3766.

    CAS  Commodity  Google Scholar

22. Hujoel MLA, Gazal S, Loh P, Patterson N, Cost AL. Liability threshold modeling of instance-command status and family history of disease increases clan power. Nat Genet. 2020;52:541–7.

    CAS  Article  Google Scholar

23. Sebastiani P, et al. A family longevity choice score: ranking Sibships by their longevity, size, and availability for study. Am J Epidemiol. 2009;170:1555–62.

    Article  Google Scholar

24. Kerber RA, Brien EO, Smith KR, Cawthon RM. Familial excess longevity in Utah genealogies. J Gerontol Ser A Biol Sci Med Sci. 2001;56:130–9.

    Article  Google Scholar

25. Rozing MP, Houwing-Duistermaat JJ, Slagboom PE, et al. Familial longevity is associated with decreased thyroid function. J Clin Endocrinol Metab. 2010;95:4979–84.

    CAS  Article  Google Scholar

26. van der Meulen A. Life tables and survival analysis. Tech report. Holland: CBS; 2012. https://www.cbs.nl/NR/rdonlyres/C047245B-B20E-492D-A4119F298DE7930C/0/2012LifetablesandSurvivalanalysysart.pdf.

    Google Scholar

27. Mandemakers K. Historical sample of kingdom of the netherlands. In: Hall PK, McCaa R, Thorvaldsen G, editors. Handbook of International Historical Microdata for Population Enquiry; 2000. p. 149–77.

    Google Scholar

28. van den Berg N, et al. Families in comparison: an individual-level comparing of life course and family unit reconstructions betwixt population and vital event registers. SocArXiv. 2018. https://osf.io/preprints/socarxiv/h2w8t/.

29. Mandemakers, Thou. 2010. https://socialhistory.org/en/hsn/hsn-releases. HSN 2010.01 release.

30. Mandemakers K, Munnik C. Historical Sample of the Netherlands. Projection Genes, Germs and Resource. Dataset LongLives. Release 2016.01. International Plant of Social History. https://pure.knaw.nl/portal/en/datasets/historical-sample-of-the-netherlands-project-genes-germs-and-reso.

31. Gavrilova NS, Gavrilov LA. When does human longevity start?: demarcation of the boundaries for human longevity. Rejuvenation Res. 2001;4:115–24.

    Google Scholar

Download references

Acknowledgements

Not applicable.

Funding

Mar Rodríguez-Girondo has received financial support from MTM2017–89422-P (MINECO/AEI/FEDER,UE) projection. The funders had no office in written report design, information collection and assay, decision to publish, or preparation of the manuscript.

Author information

Affiliations

1. Section of Biomedical Information Sciences, section of Medical Statistics, Leiden University Medical Heart, Albinusdreef 2, 2333, ZA, Leiden, the Netherlands

   Mar Rodríguez-Girondo

2. Department of Biomedical Information Sciences, Section of Molecular Epidemiology, Leiden University Medical Eye, Albinusdreef two, 2333, ZA, Leiden, the Netherlands

   Niels van den Berg, Marian Beekman & Eline Slagboom

3. Department of Clinical Epidemiology, Biostatistics, and Bioinformatics, Amsterdam UMC, University of Amsterdam, Meibergdreef nine, 1105, AZ, Amsterdam, the Netherlands

   Michel H. Hof

Contributions

G.R.G. and Grand.H.P.H. conceived the new mLRC method. Thousand.R.G. performed the computations and data analysis. Northward.v.d.B. preprocessed existent data and participated in real data analysis. One thousand.B. and E.P.S. supervised the findings of this work. All authors discussed the results and contributed to the final manuscript. The author(s) read and approved the final manuscript.

Corresponding author

Correspondence to Mar Rodríguez-Girondo.

Ethics declarations

Ideals approval and consent to participate

No permission from the ethical medical commission was required to collect and analyzed the HSN data. The authors got formal permission to analyze and publish the data from the International Institute for Social History (IISG).

Consent for publication

Non applicable.

Competing interests

The authors declare that they have no disharmonize of interest.

Boosted information

Publisher'due south Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Rights and permissions

Open Access This article is licensed nether a Creative Commons Attribution 4.0 International License, which permits apply, sharing, adaptation, distribution and reproduction in whatever medium or format, as long as you give appropriate credit to the original writer(south) and the source, provide a link to the Creative Eatables licence, and indicate if changes were made. The images or other third party material in this article are included in the article'due south Artistic Commons licence, unless indicated otherwise in a credit line to the cloth. If fabric is not included in the article'south Creative Eatables licence and your intended use is not permitted by statutory regulation or exceeds the permitted utilise, you will need to obtain permission straight from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/i.0/) applies to the information fabricated bachelor in this article, unless otherwise stated in a credit line to the data.

Reprints and Permissions

Well-nigh this article

Cite this commodity

Rodríguez-Girondo, M., van den Berg, Due north., Hof, 1000.H. et al. Improved selection of participants in genetic longevity studies: family unit scores revisited. BMC Med Res Methodol 21, seven (2021). https://doi.org/10.1186/s12874-020-01193-seven

Download citation

• Received: 03 June 2020

• Accepted: fourteen December 2020

• Published: 06 Jan 2021

• DOI : https://doi.org/10.1186/s12874-020-01193-7

Keywords

• Longevity
• Mixed effects modelling
• Family history score
• Family size

cochranhoset1953.blogspot.com

Source: https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-020-01193-7

Share this post